1. Introduction
2. The purpose of the RasterImage class
3. Housekeeping methods.
4. Reflection methods
5. Rotation methods
6. Image zooming methods
7. Miscellaneous methods
8. Conclusions
1. Introduction
Like the last chapter, the focus in this chapter will be on the methods within a class. The set of methods in a class collectively define the essence of the class, its raison d’être.
For example, in a class to simulate a four-function calculator we would expect to find the following public methods: add(), subtract(), multiply() and divide() . This set of cohesive methods will operate on some private underlying data, typically a numeric datatype. A consequence of the principle of Information Hiding is that a user of the class does not need to know about (i.e. abstraction) or is able to know about the underlying data (i.e. encapsulation).
This chapter completes the description of the elements of object oriented programming (OOP) concepts and syntax in the graphics language called Processing. In the next chapter these elements will be put to use in order to construct a complete class.
The methods that will be described in this chapter will use more complex argument lists (i.e. diverse types and numbers of arguments) and the elements of the argument lists will be more complex in the sense that they will sometimes be aggregates of data (e.g. Array, Object and String) each of which can hold multiple data elements.
By the end of this chapter you will understand how to use existing methods and develop new methods with complex argument lists and argument datatypes.
2. The purpose of the RasterImage class
The purpose of the class that will be described in this chapter (i.e. RasterImage) is to provide a set of basic image processing methods that will operate on the one property in the class. The property is an instance of another class called PImage . The RasterImage class has capabilities similar to applications like Photoshop™ or Paint Shop Pro™ and could become a platform for building a real application.
The image in the top left hand corner of Figure 1 (left-hand pane) is an example of a PImage object. It has been used to initialise the property of an instance of the class RasterImage (i.e. an object) for the example code in this chapter. The other eleven images are new images returned by various RasterImage methods in the class and demonstrate various transformations of the original property. For example:
- left-hand pane: reflection of the original property about the horizontal (X) and/or vertical (Y) axis,
- middle pane: rotation of the original property through 0°, 90°, 180° and 270° and
- right-hand pane: zooming of the top-left, top-right, bottom-left and bottom-right quarters of the original property which collectively form an enlargement of the property.
The class PImage was described briefly in Greenberg (2007, chapter 6) and will be described in more detail in a later chapter of this book.
For now all we need to know about the PImage class is the following:
- An image (e.g. gif, jpg, png etc…) can be loaded from a file and can be rendered on screen.
- An image consists of a two-dimensional array of pixels where a pixel is a numeric value corresponding to a colour. Pixels will also be described in detail in a later chapter of this book.
- The origin (i.e. X=0, Y=0) of an image is the top left hand corner. The Y values increase numerically moving down the image and the X values increase numerically moving rightwards across the image.
- An image has a number of properties but for now we are only interested in the pixels in the image plus the width and height of the image (measured as a number of pixels).
There are many useful and powerful methods defined in the class PImage some of which will provide an alternative (and possibly better) mechanism for implementing the transformations demonstrated in this chapter. However, the power of image processing will be demonstrated using variations on the theme of nested iteration statements and using a subset of the available PImage methods which includes the following:
- To create a new instance of a PImage where the pixels are loaded from a file e.g. PImage ouLogo = loadImage(“ouLogo.png”);
- To render an image on screen at a specific X and Y location (of type int) e.g. image(ouLogo, X, Y);
- The image has fixed properties of width and height (of type int) e.g. ouLogo.width and ouLogo.height respectively. These values are defined when using loadImage() where they are based on the loaded image or new() where they are provided as input argument values.
- The pixel at a specific X and Y location may be obtained using a getter method e.g. ouLogo.get(X, Y);
- The pixel at a specific X and Y location may be set to a new pixel value (of type color) using a setter method e.g. ouLogo.set(X,Y,aColor);
- To create a new instance of a PImage (with a specified height and width) where the pixels can be initialised later using set() e.g. PImage ouLogo = new PImage(width, height);
Figure 2 shows the two classes used in the examples in this chapter, shown in a UML class diagram. The RasterImage class is a user-written class and PImage is a utility class provided as part of the Processing environment.
Readers familiar with the UML will recognise that the diagram is a specification of what you need to know in order to be able to use the class RasterImage .
Readers unfamiliar with the UML should be able to deduce the following from the diagram:
- it provides a summary of methods in the class RasterImage and
- the methods use complex (aggregate) data e.g. PImage, String, int[ ], String[ ], PImage[ ] which is passed in to and out of the methods defined in the class RasterImage. Some of these methods will now be described in detail.
3. Housekeeping methods.
The upper frame of Figure 3 shows how a RasterImage object is created and rendered on screen. A constuctor (shown in the lower frame) with a single argument of String type is used to to specify an image filename (e.g. “ouLogo.png” ). We shall assume that the image file does exist and is located in the same folder as the code in the figure. Within the constructor the loadImage() function is invoked to initalise the single property in the class called image. A getter method i.e. getImage() returns the initialised PImage object. The image is not rendered on screen until the image() function is invoked, where the first actual argument is a PImage object and the other actual arguments are the X and Y coodinates of the top left hand corner of the image e.g. 0,0. Notice that the image properties of width and height are returned through the methods getImageHeight() and getImageWidth() which are then used to intialise the window size in the calling code using the size() function.
Apart from the use of the aggregate data types PImage and String the object oriented code in Figure 3 should be starting to look increasingly familiar.
We shall now extend the class with some methods that make use of another form of aggregate data, the array. The method getImageDimensions() is shown below and demonstrates that it is possible to return an array as a result from a method. Note the use of square brackets for arrays, rather than round or curly brackets.
public int [ ] getImageDimensions(){
int[] result={getImageWidth(),getImageHeight()};
return result;//returns a 2-element array of ints
} We are limiting our interest to the two integer values corresponding to the width and height properties of the PImage object but if there was a need, we might have obtained more property values and returned an array of a larger dimension.
The implementation code for the getImageDimensions() method shows that it is possible to initialise array elements in an array declaration statement using an initialiser statement i.e. the code within the curly brackets. The array dimension is determined by the number of initialised elements in the initialiser e.g.
int[] result={getImageWidth(),getImageHeight()}; Later examples in this chapter will show how to determine the array dimension dynamically, however, for this example we know the array dimension is two. The calling code may then use the elements of the array returned by the method getImageDimensions() as follows:
int[] imageProperties;
//declare array in the calling program
imageProperties=ouLogo.getImageDimensions();
//initialise array
println ("Width: " + imageProperties[0] +
" , Height: " + imageProperties[1]);
A common mistake made by novice programmers is to forget that the elements of an array are indexed from zero (many computer languages index from one). Thus in the code excerpt immediately above, any attempt to access an element with an index greater than one (or less than zero) will result in a run-time crash of the program.
Another common mistake is to use the array after it has been declared but before has been initialised, for example, if the second and third statements were swapped in the code above i.e. the assignment and output statements. Fortunately, the compiler will alert us to this problem by displaying an error message during compilation.
4. Reflection methods
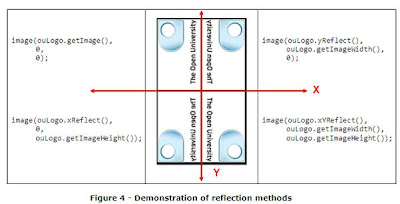Figure 4 illustrates the three RasterImage reflection methods, which act as symmetrical mirrors in one or two dimensions acting on the original property returned by the method getImage() . The code shown adjacent to the figure shows how the methods might be invoked i.e.: - yReflect() reflects the RasterImage property about the vertical axis i.e. Y ,
- xReflect() reflects the RasterImage property about the horizontal axis i.e. X and
- xYReflect() reflects the RasterImage property about both the horizontal axis and the vertical axis i.e. X and Y .
Since the image property of the RasterImage class is a two-dimensional (2-D) array of pixels, all the reflection methods are coded following the same algorithm:
- A new PImage object is created with the same dimensions as the property of the class.
- A nested pair of iteration statements systematically accesses all the source pixels i.e. using get():
- Each source pixel is copied into the new image i.e. using set() with a pair of index values that (usually) differ from the source.
- When all the source pixels have been mapped to the new PImage , the new object is returned from the method.
The mapping of the source to destination pixels requires some thought and probably is best done with pen and paper first. Figure 5 shows a three by three array of pixels, representing a scaled down version of the source image (left) and the destination image (right).
Table 1 shows the mappings for the vertical reflections produced by yReflect(). The column on the left represents the row and column index values for the source pixel and the column on the right represents the row and column index values for the destination of that pixel.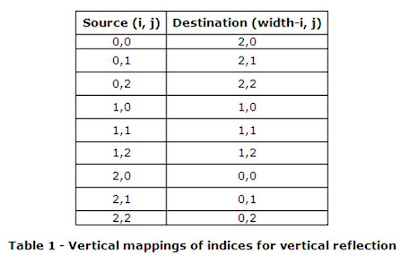
The implementation code for reflection about the vertical axis method i.e. yReflect() is show below - the “devil is in the detail!”. Note that the first argument to set() is decremented by one because the value of width is one more that the largest index value i.e. width-1 .
The two loop index variables i and j are used to systematically get every source pixel one by one. The pixel is then copied through to the new image at a computed location that depends on the image width and the index variables.
private PImage yReflect(){
// reflection about the Y-axis
PImage newImage = new PImage(getImageWidth(),
getImageHeight());
int w = newImage.width;
int h = newImage.height;
for (int i=0; i < w; i++)
for (int j=0; j < h; j++)
newImage.set(w-i-1, j, image.get(i,j));
//change for x and x&y
return newImage;
}
The implementation code for the other two reflection methods xReflect() and xYReflect() only differ with respect to mapping of the indices for the destination of the copied pixel. Consequently only one statement in the code above has to be changed and is left as an exercise for the reader.
5. Rotation methods
A similar approach can be adopted for the rotation methods as was used for the reflection methods. That is, every pixel is mapped to a destination which is usually different from its source. There is an extra complication for the 90° and 270° rotations because the width and height of the original and new images are transposed.
The implementation code for the method rotate90() is shown below and apart from the transposing of the original image properties for the new image, the code resembles the reflection methods.
private PImage rotate90(){
// rotation through 90 degrees
PImage newImage=new PImage(
getImageHeight(),
getImageWidth());//transposed
int w = newImage.width;
int h = newImage.height;
for (int i = 0; i<w; i++)
for (int j = 0; j<h; j++)
newImage.set(
getImageHeight()-i-1,
getImageWidth()-j-1,
image.get(getImageWidth()-j-1,i));
return newImage;
}
Closer examination of Figures 4 and 6 reveals that:
- The methods rotate180() and xYReflect() produce the same visual appearance and
- The method rotate270() and the ordered sequence of methods of rotate90(), xReflect() and xYReflect() collectively produce the same visual appearance, c.f. Figure 7.
Thus it is possible to implement the rotate180() method as follows:
private PImage rotate180(){
// rotation through 180 degrees
return xYReflect();
}
Before we can implement rotate270() using existing methods we need to introduce a new constructor that has a single PImage argument as shown below. The constructor creates a new RasterImage object with its property initialised by copying through the pixels values of the formal argument i.e. original :
public RasterImage(PImage original){
image = new PImage(original.width,
original.height);
int w = image.width;
int h = image.height;
for (int i=0; i < w; i++)
// copy every pixel from source to dest.
for (int j=0; j < h; j++)
image.set(i, j, original.get(i, j));
}As shown below, the new constructor is used to create temporary RasterImage objects in the implementation code for the rotate270() method. Methods are invoked on the temporary RasterImage objects that return PImage objects which are then used as the actual argument to the next use of the new constructor. The cascade of image transformations (shown in Figure 7) leads to the desired outcome.
private PImage rotate270(){
// rotation through 270 degrees
RasterImage rotated90
= new
RasterImage(rotate90());
RasterImage rotated90AndXReflected
= new
RasterImage(rotated90.xReflect());
RasterImage rotated90AndXReflectedAndYReflected
= new
RasterImage(rotated90AndXReflected.yReflect());
return rotated90AndXReflectedAndYReflected.getImage();
}
The implementation code for this method illustrates that we should always be alert to the possibility of code reuse.
6. Image zooming methods
The zooming of an image requires the definition of a zoom rectangle (the inner rectangle in Figure 8) which is a sub-section of the original image. The pixels within the zoom rectangle must then be used to fill the program window (the outer rectangle in Figure 8). Since the area of the program window is greater than the area of the zoom rectangle there has to be an expansion which means each pixel within the zoom rectangle will be mapped to more than one location in the program window. The mapping function will be described soon.
The RasterImage class has methods called topLeft(), topRight(), bottomLeft() and bottomRight() each of which each define a zoom rectangle corresponding to exactly one quarter of the original image (a quadrant). The method names reveal the location of the zoom rectangle relative to the original image in other words which of the four quadrants that will be zoomed.
Each pixel in the zoom rectangle is used more than once in the grid of pixels that appear in the program window. How many times the source pixel is used depends on the degree of zooming. For example, if we consider a single line of pixels and source the first half of the line (on the left), as we do in topLeft() then each source pixel is copied to two adjacent pixel locations on the destination line so that we fill the entire line in the resultant zoomed image.
Figure 9 demonstrates how the four new images collectively produce an enlarged version of the original image.
The four quadrant methods each invoke another more general purpose method called zoom() which has two pairs of arguments corresponding to the coordinates of the top-left corner and bottom-right corner of the zoom rectangle.
For the topLeft() method, the top left corner of the zoom rectangle is the same as the top-left corner of the original image i.e. 0, 0 and the bottom-right corner of the zoom rectangle is the centre of the original image i.e. (getImageWidth()/2)-1, (getImageHeight()/2)-1
The implementation code for the method topLeft() is shown below:
private PImage topLeft(){
// top left quadrant
return zoom(0, 0,
(getImageWidth()/2)-1,
(getImageHeight()/2)-1);
}
The other three quadrant methods are left as an exercise for the reader.
To understand how to code the zoom() method it is necessary to understand the geometry for the mapping of a point in the program window from an equivalent point in the zoom rectangle.
Referring to Figure 8 we need to define a mapping function that relates the point I, J in the program window with the point X, Y in the zoom rectangle.
If we consider the horizontal axis first, then we observe that the ratio of I relative to the window width has to be the same ratio as X relative to the zoom rectangle width i.e.
Rearranging the equation above gives the value for the horizontal distance of the point in the zoom rectangle relative to the start of the zoom triangle i.e.
The value for the horizontal distance of the point in the zoom rectangle relative to the start of the program window gives:
If
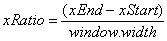then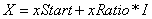
A similar equation can be derived for the vertical coordinate of the point in the zoom triangle i.e.If
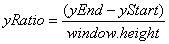
then
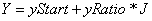We now have mapping equations where a point I,J in the program window can be mapped from a point X,Y in the zoom triangle.The zoom() method iterates through every value for a point I,J in the program window and copies a pixel from the computed X,Y point in the zoom triangle.
The implementation code for the zoom() method is shown below. The calculation of the X and Y values involves mixed-datatype expressions i.e. integer and floating point numbers. The resulting expression will be a floating-point datatype, so to convert the result into an integer datatype (to be used as an index) the built-in function round() is used. The function returns the nearest integer value corresponding to the floating-point argument.
private PImage zoom (int xStart, int yStart,
int xEnd, int yEnd){
PImage newImage = new PImage(
getImageWidth(),
getImageHeight());
int w = newImage.width;
int h = newImage.height;
float xRatio = float(xEnd-xStart)/w;
// Note: int/float -> float
float yRatio = float(yEnd-yStart)/h;
for (int i = 0; i < w; i++)
for (int j = 0; j < h; j++)
newImage.set(i, j,image.get(
round(xStart + (i * xRatio)),
round(yStart + (j * yRatio))));
return newImage;
}
The approach described above where a single source pixel in the zoom triangle is mapped to the zoomed image can lead to ragged images. More sophisticated techniques use smoothing algorithms. For example, taking an average pixel numeric value from all the points around the source pixel (including the source pixel) in the zoom rectangle.
There are many algorithms for doing image smoothing but they are outside the scope of this book. It is left as an exercise for the reader to investigate further, if interested.
7. Miscellaneous methods
We conclude this chapter by introducing another method called getImages() , that returns a variable sized array of PImage objects. The actual objects returned depends on the string values in a variable sized array of strings passed into the method. Since we can not anticipate the size of the array of strings, we need to use the length property of the array to discern its size. This is demonstrated in the first executable statement in the implementation code shown below. Once we know the number of strings we can allocate memory for the array of PImage objects as shown in the second executable statement. The array will then be initialised and returned from the method.
public PImage[] getImages (String [] list){
int len = list.length; // get array length
PImage[] theImages = new PImage[len];
for (int i=0; i < len; i++)
theImages[i] = getNextImage(list[i]);
return theImages;
}
The body of the iteration statement above passes an indexed element of the array of strings into another method called getNextImage() which returns the PImage object corresponding to the string. If the input string is unrecognised then the PImage property value is returned as a default value.private PImage getNextImage(String s){
if (s == "XREFLECT")
return xReflect();
else if (s == "YREFLECT")
return yReflect();
else if (s == "XYREFLECT")
return xYReflect();
else if (s == "ROTATE0")
return image;
else if (s == "ROTATE90")
return rotate90();
// etc…
else if (s == "TOPRIGHT")
return topRight();
else if (s == "BOTTOMLEFT")
return bottomLeft();
else if (s == "BOTTOMRIGHT")
return bottomRight();
else
return image;
}
The code shown below demonstrates how we might use the method getImages() . The code demonstrates that an array of strings called requests is initialised in an initialiser statement. The array is passed into the method when getImages() is invoked. The output from the method is an array of PImage objects of the same dimension as the input string dimension. The array property length is used to determine the array dimension. The first iteration statement is used to work out the maximum width for the set of requested images (remember the width and length do not have to be equal) and also determines the maximum length of all the images with a small gap between the images. These two values are then used to define the dimensions of the program window.The second iteration statement then renders the images one by one which is presented as a single column of images. The width and height of a PImage object are public properties of the PImage class. The later is used in the placement of each image within the window.
RasterImage ouLogo = new RasterImage("ouLogo.gif");
String [] requests =
{"XREFLECT", "DEFAULT", "ROTATE270"};
// Note: unrecognised strings default to getImage()
PImage [] theImages = ouLogo.getImages(requests);
int len = theImages.length;
int maxWidth = 0;
// the width of the widest image
int totalHeight=0;
// accumulative height of all the images inc. a gap
int yGap=10;
// a small vertical gap between each image
for (int i=0; i < len; i++){
if (theImages[i].width > maxWidth)
maxWidth = theImages[i].width;
// update maximum width
totalHeight += yGap + theImages[i].height;
// update total height
}
size(maxWidth, totalHeight);
int currentDisplayHeight = 0;
// current height for rendering image
for (int i=0; i < len; i++){
image(theImages[i], 0, currentDisplayHeight);
currentDisplayHeight += yGap + theImages[i].height;
}
8. Conclusions
The methods in the RasterImage class now provide a platform of basic housekeeping methods e.g. constructors, getters/setters and a set of application methods e.g. reflections, rotations and zooming.
In this chapter we have looked at many of the methods in a class for processing images. These methods have used more complex forms of data including instances of the classes PImage and RasterImage as well as arrays of integers, strings and objects. This concludes the description of the basic details needed to write an object oriented program in Processing. The next chapter will put to use the contents of this chapter and the previous chapters in order to write a complete object oriented class.
References:
GREENBERG, IRA (2007), Processing – Creative Coding and Computational Art, APress
